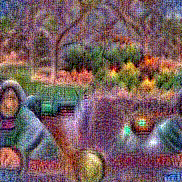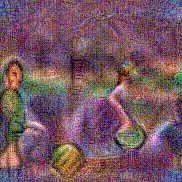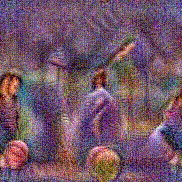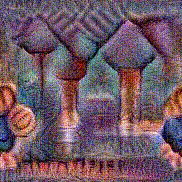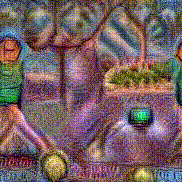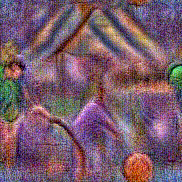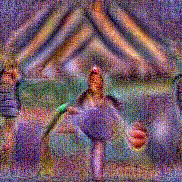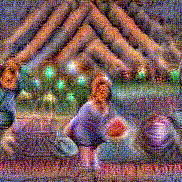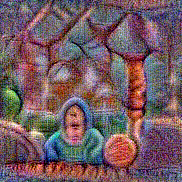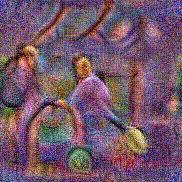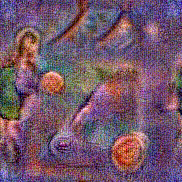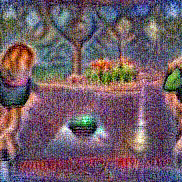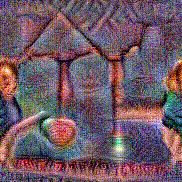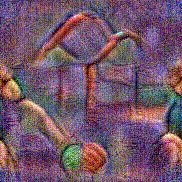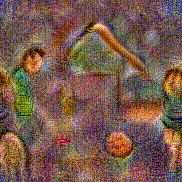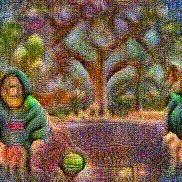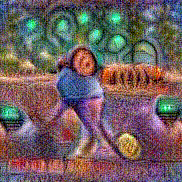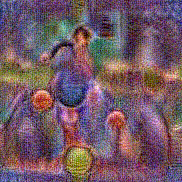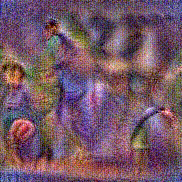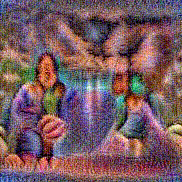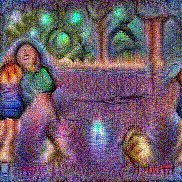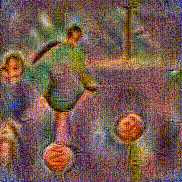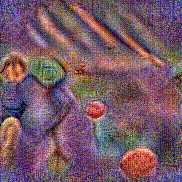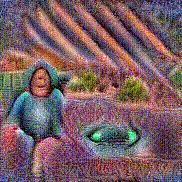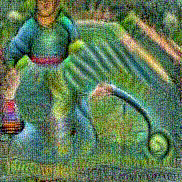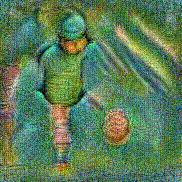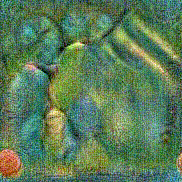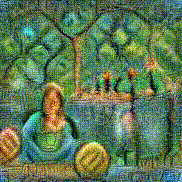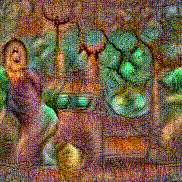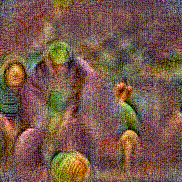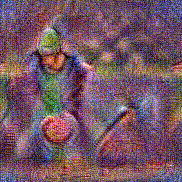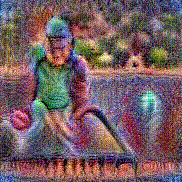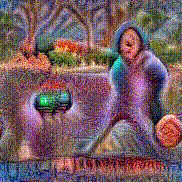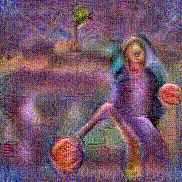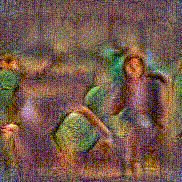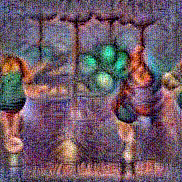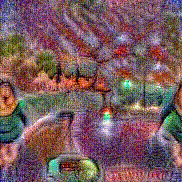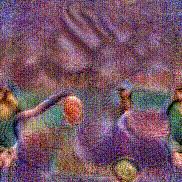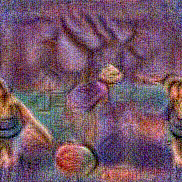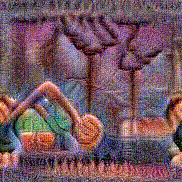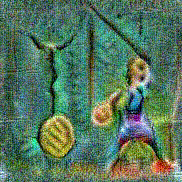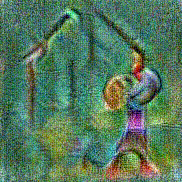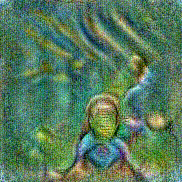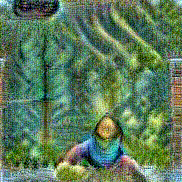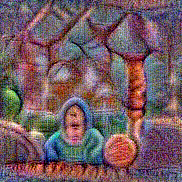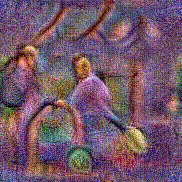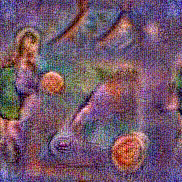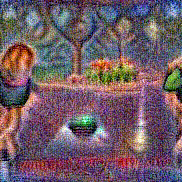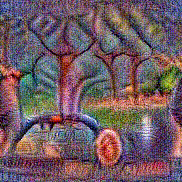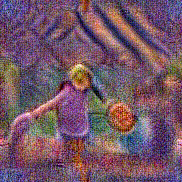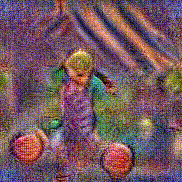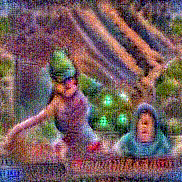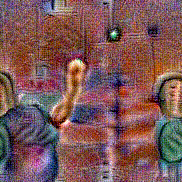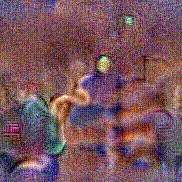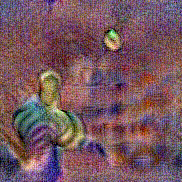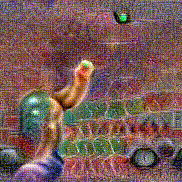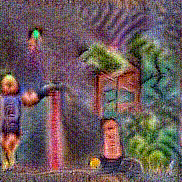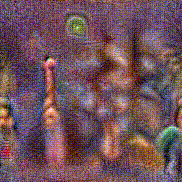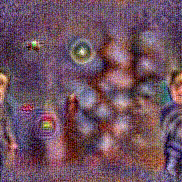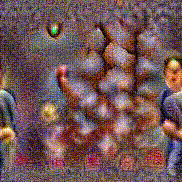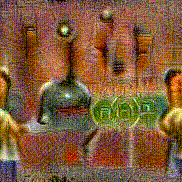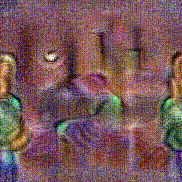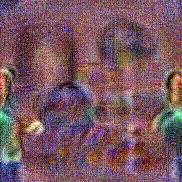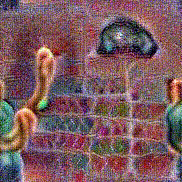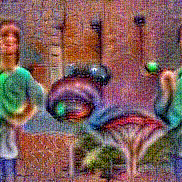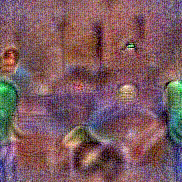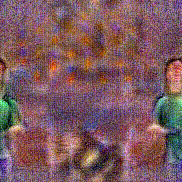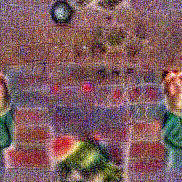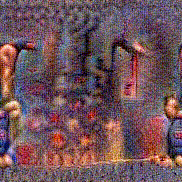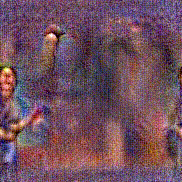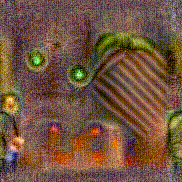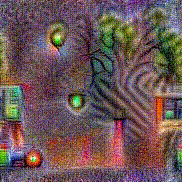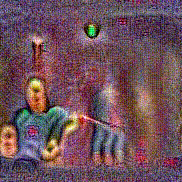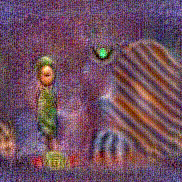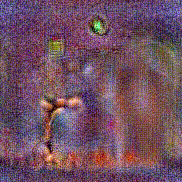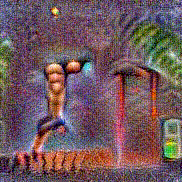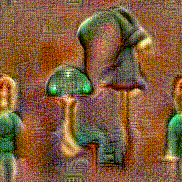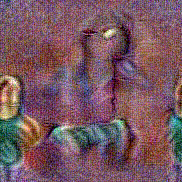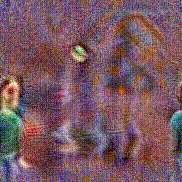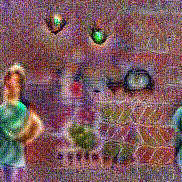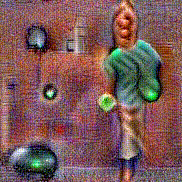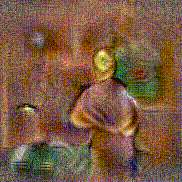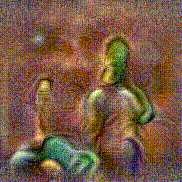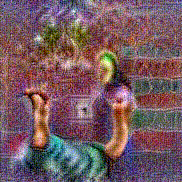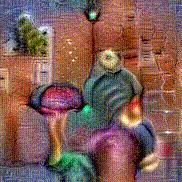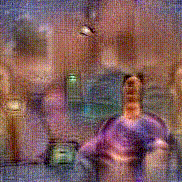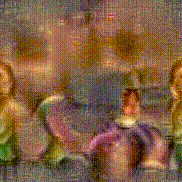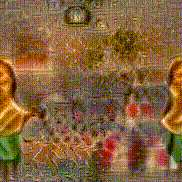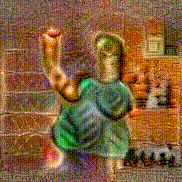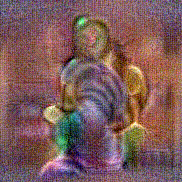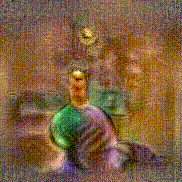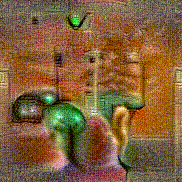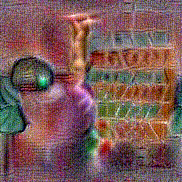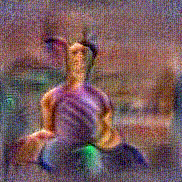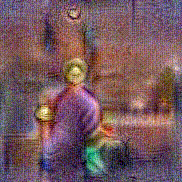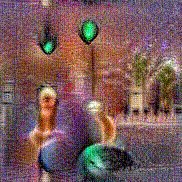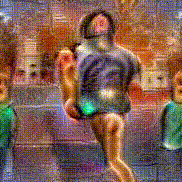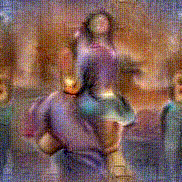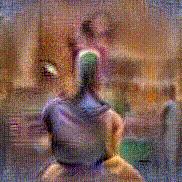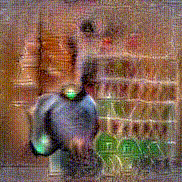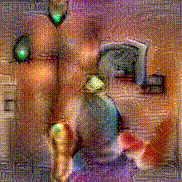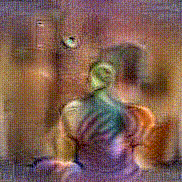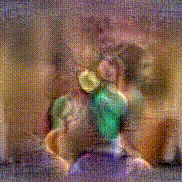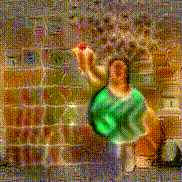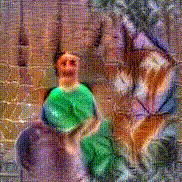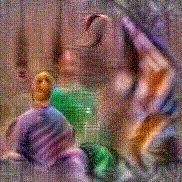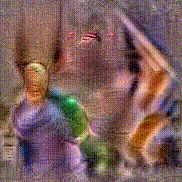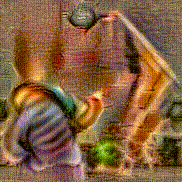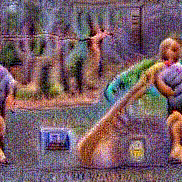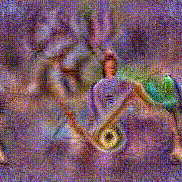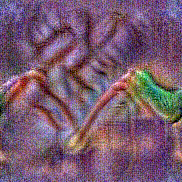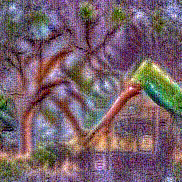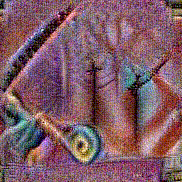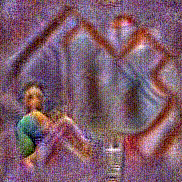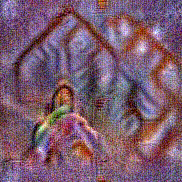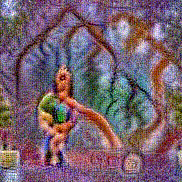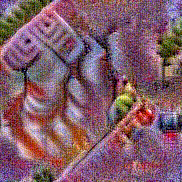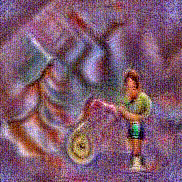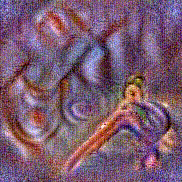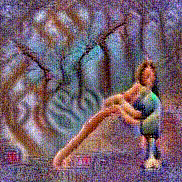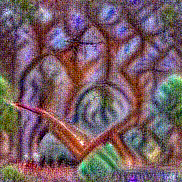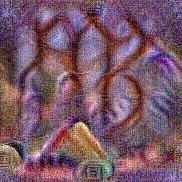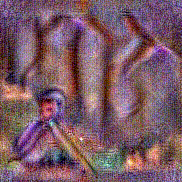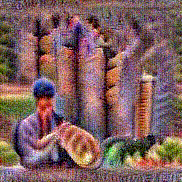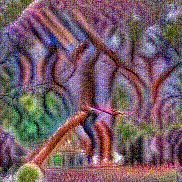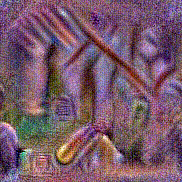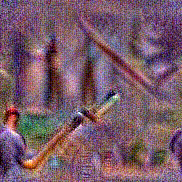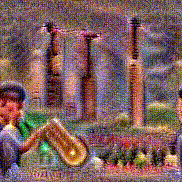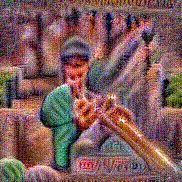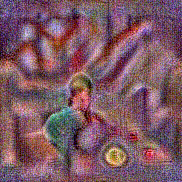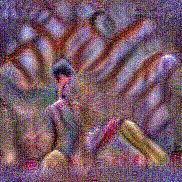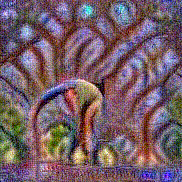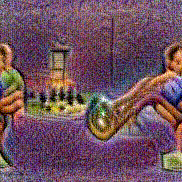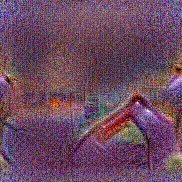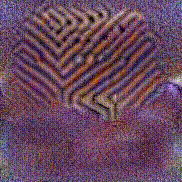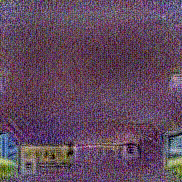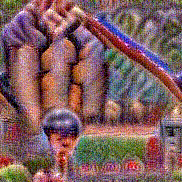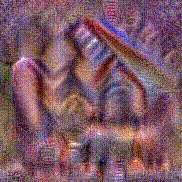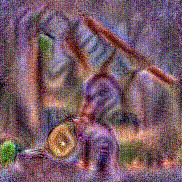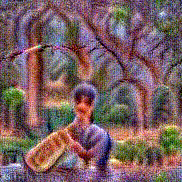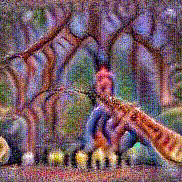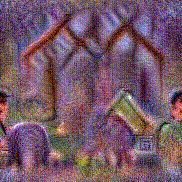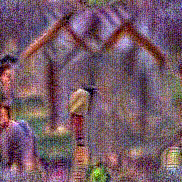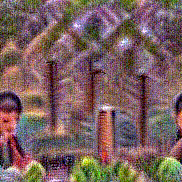Leaping Into Memories: Space-Time Deep Feature Synthesis

ICCV 2023

    Vrije Universiteit Brussel & imec      



Abstract

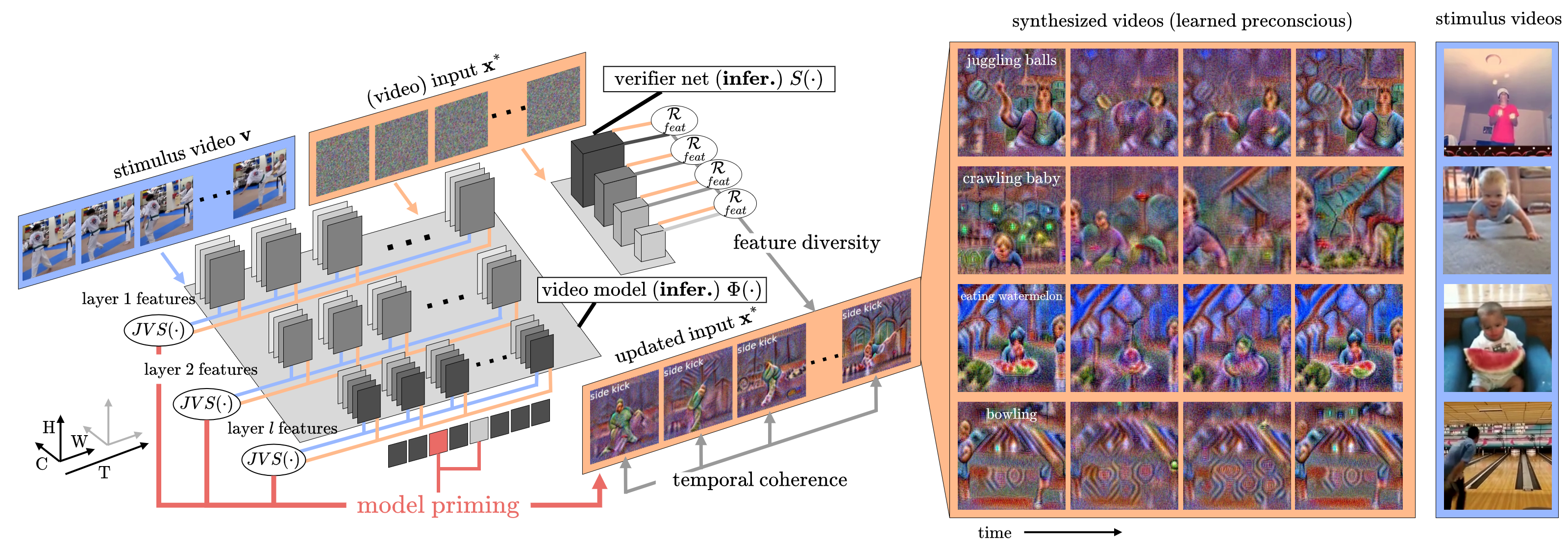
The success of deep learning models has led to their adaptation and adoption by prominent video understanding methods. The majority of these approaches encode features in a joint space-time modality for which the inner workings and learned representations are difficult to visually interpret. We propose LEArned Preconscious Synthesis (LEAPS), an architecture-independent method for synthesizing videos from the internal spatiotemporal representations of models. Using a stimulus video and a target class, we prime a fixed space-time model and iteratively optimize a video initialized with random noise. Additional regularizers are used to improve the feature diversity of the synthesized videos alongside the cross-frame temporal coherence of motions. We quantitatively and qualitatively evaluate the applicability of LEAPS by inverting a range of spatiotemporal convolutional and attention-based architectures trained on Kinetics-400, which to the best of our knowledge has not been previously accomplished.


Video overview

Synthesized videos


Use the arrows to navigate over synthesized videos from different inverted models.


Stimuli

Stimulus video

       
Stimuli

Stimulus video

       
Stimuli

Stimulus video

       

Method


Model priming

Motivated by visual priming in cognitive science, we demonstrate that learned representations of video models can become accessible through model priming. By using a video stimulus \( \mathbf{x} \) and a parameterized input \( \mathbf{x}^{*} \), we iteratively synthesize the dominant learned concepts corresponding to actions. We define a priming loss based on the difference between internal representations inferred from the stimulus video and those from the optimized across model layers. $$ \underset{prim}{\mathcal{L}}(\mathbf{x}^{*},\mathbf{v}) \! = \!\! \; \frac{1}{L} \sum_{l \in \mathbf{\Lambda}} \lambda_{l} \; JVS \left( \mu \!\left( \textbf{z}^{l}(\mathbf{x}^{*}) \right) \!,\mu \!\left(\textbf{z}^{l}(\mathbf{v})\right) \right) $$ where \( \mu \!\left( \textbf{z}^{l}(\mathbf{x}) \right) \) and \( \mu \!\left( \textbf{z}^{l}(\mathbf{x}^{*}) \right) \) are mean embeddings vectors for the stimulus and parameterized input for all layer \(l \in \mathbf{\Lambda} \) layers . We use denotes the Jaccard vector similarity \( JVS(\cdot) \) to compare them. Due to the vastness of the feature space when optimizing the input, we include two additional regularization terms as constraints.


Temporal Coherence Regularization

Fig1
For the first regularizer, we aim to enforce similarity between representations of consecutive frames in order to enable consistent feature transitions in the synthesized video. Therefore, we include a coherence regularizer. We use embeddings \( \mathbf{z}^{L}(\mathbf{x}^{*})_{t_1} \) and \( \mathbf{z}^{L}(\mathbf{x}^{*})_{t_2} \) at temporal locations \(t_1\) and \(t_2\). For consecutive \(t_1\) and \(t_2\) locations we enforce similarity while we increase their divergence in non-consecutive cases. $$ \underset{coh}{\mathcal{R}}(\mathbf{x}^{*}) \! = \! \begin{cases} || \mathbf{z}^{L}(\mathbf{x}^{*})_{t_1} \! - \! \mathbf{z}^{L}(\mathbf{x}^{*})_{t_2} ||_1 , \text{if consecutive}\\ \text{max}\!\left( 0,\delta \! - \!|| \mathbf{z}^{L}(\mathbf{x}^{*})_{t_1} \! - \! \mathbf{z}^{L}(\mathbf{x}^{*})_{t_2} ||_1 \right) \! , \text{elsewise} \end{cases} $$ Although the regularizer can be applied to any layer, in practice, using all layers enforces a very strong regularization, producing synthesized videos with minimal to no cross-frame variations (effect shown at the figure at the right).

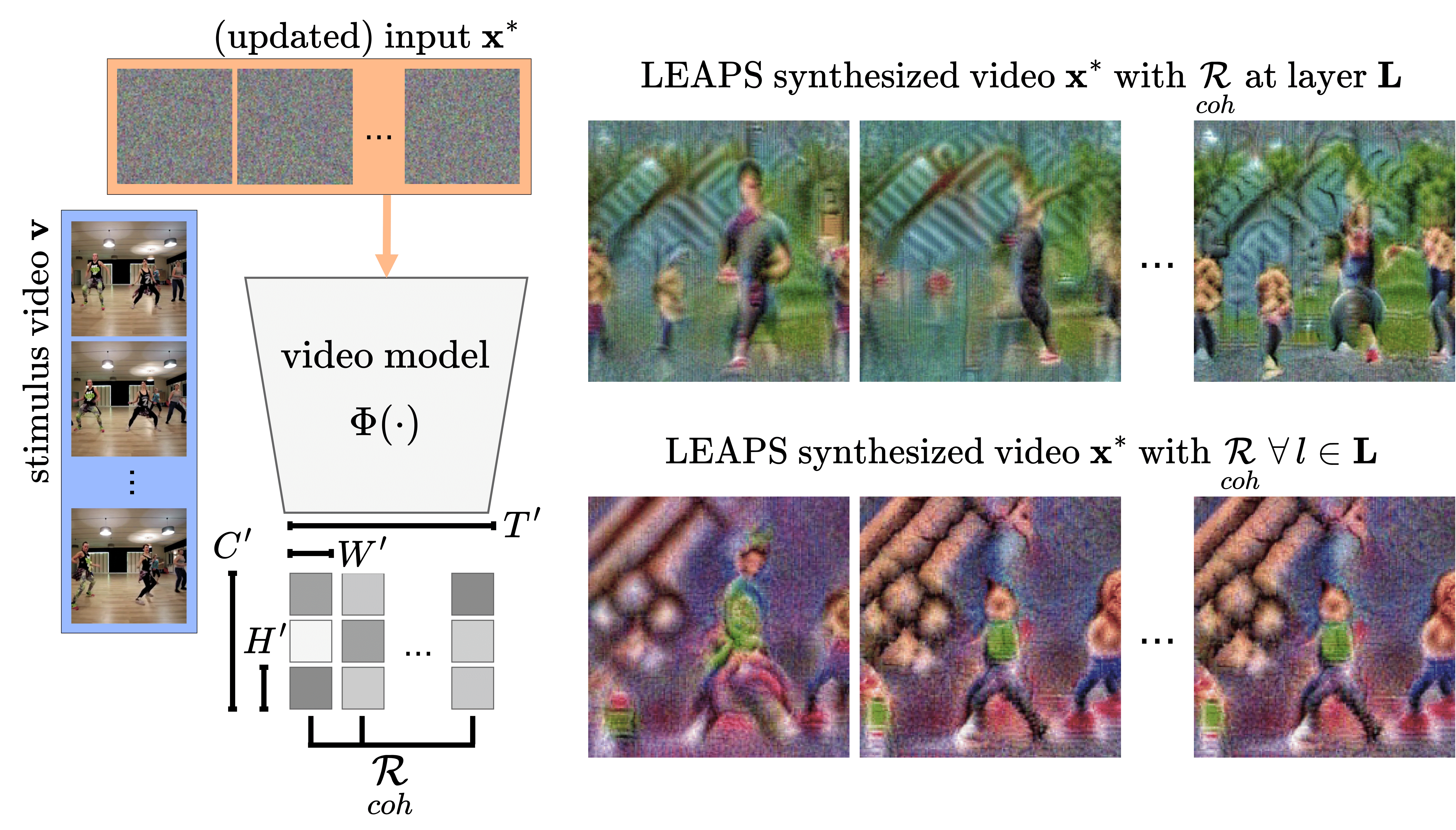
Feature Diversity Regularization

Despite priming providing a strong signal with which the input can be updated, the diversity of features is limited compared to observing multiple instances. Thus, class features varying from those in the stimulus, or features not present in the stimulus, may not be explored during optimization. To enhance the search space we include an additional domain-specific verifier network and feature diversity regularizer. We use the batch norm mean and variance to approximate the expected mean and variance.


The final LEAPS objective if formulated as the combination of model priming, temporal coherence, and feature diversity regularizers. $$ \mathcal{L}(\mathbf{x}^{*},\mathbf{v}, y) \! = \! \underset{CE}{\mathcal{L}}(\mathbf{x}^{*},y) + \underset{prim}{\mathcal{L}}(\mathbf{x}^{*},\mathbf{v}) + r \mathcal{R}(\mathbf{x}^{*}) $$

Citation

@inproceedings{stergiou2023leaping,
title={Leaping Into Memories: Space-Time Deep Feature Synthesis},
author={Stergiou, Alexandros and Deligiannis, Nikos},
booktitle={IEEE/CVF International Conference on Computer Vision (ICCV)},
year={2023}}